Calculo vectorial
Castillo Vigueras Ricardo
Rodríguez Briones David
García Ruiz Marisol
Díaz Villafaña Alejandro

VECTORES

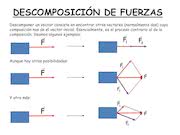
DESCOMPOSICIÓN DE FUERZAS
Descomponer un vector consiste en encontrar otros vectores (normalmente dos) cuya
composición nos de el vector inicial. Esencialmente, es el proceso contrario al de la
composición. Veamos algunos ejemplos:




F

Aunque hay otras posibilidades:


F

F1

F2


F1

F

F2

Y otra más:


F


F1


F

F2

DESCOMPOSICIÓN DE FUERZAS
Entonces, ¿cuál es la forma correcta de descomponer un vector? Pues todas. En
realidad hay infinitas maneras de descomponer un vector y todas son correctas pues
cumplen la definición de descomposición vectorial.
Nosotros vamos a estudiar una llamada DESCOMPOSICIÓN NORMAL, en la que los
vectores obtenidos (componentes), son perpendiculares entre sí.
y


F

y


F


Fy

x


Fx


Fy
De forma que…

Fx = componente x
Fy = componente y

F



Fx

F2  Fx2  Fy2

Fy

sen α 

cos  

Fy
F

Fx
F


F

Fy  F·sen 

Fx  F·cos 


Fx

x

DESCOMPOSICIÓN DE FUERZAS
Vamos a ver ahora una aplicación práctica de la descomposición de vectores: el
desplazamiento sobre un plano inclinado.
Nos centraremos, concretamente, en la descomposición de la fuerza-peso. Esta fuerza
tiene dos efectos sobre el cuerpo que se desplaza: lo mantiene en contacto con la
superficie del plano inclinado y lo empuja hacia abajo.
Cada uno de estos dos efectos es debido a las dos componentes de la fuerza-peso:

Px

y


Px

Py




Py







P

x


P


Px


P

Px = componente tangencial del peso
Py = componente normal del peso




Py

sen  

cos  

P

Px

Py

PX
P
Py
P

Px  P·sen α

Py  P·cos 

Ecuaciones rectas y planas

• Una recta en el plano xy esta determinada
cuando se dan un punto y una dirección sobre
su recta. La ecuación de la recta puede
expresarse utilizando la forma puntopendiente

• De manera semejante una recta “L” en el
espacio tridimensional esta determinada
cuando sabemos un punto Po( Xo, Yo, Zo ),
sobre L y la dirección de L. La dirección de una
recta se describe de manera conveniente por
un vector, así v es un vector paralelo a L. Sea
P(x,y,z) un punto arbitrario sobre L y sean r0 y
r los vectores posición de Po y P

• La ecuación vectorial de L. Cada valor del
parámetro t proporciona el vector posición r
de un punto sobre L. Los valores positivos de t
corresponden a los puntos de L que están del
lado de Po, en tanto que los valores negativos
de t corresponden a los puntos que están del
otro lado de Po.

1.7 APLICACIONES FISICAS Y GEOMETRICAS
DE LOS PRODUCTOS ESCALARES Y
VECTORIALES
Aplicación: ángulo entre dos vectores (producto escalar): El producto escalar de
dos vectores es por definición un escalar.
𝑎 . 𝑏 = 𝑎 . 𝑏 . cos 𝛼
Propiedades:
𝑎 · 𝑏 = 𝑏 · 𝑎
𝑝 · (𝑞 + 𝑟) = 𝑝 · 𝑞 + 𝑝 · 𝑟
Podemos usar ahora el producto escalar para encontrar el ángulo de los
vectores a y b:
𝑎 . 𝑏 = 𝑎 . 𝑏 . cos 𝛼
Con lo que deducimos que:
𝑎𝑥 𝑏𝑥 + 𝑎𝑦 𝑏𝑦 + 𝑎𝑧 𝑏𝑧
𝑎 .𝑏
cos 𝑎, 𝑏 =
=
𝑎. 𝑏
𝑎𝑥2 + 𝑎𝑦2 + 𝑎𝑧2 + 𝑏𝑥2 + 𝑏𝑦2 + 𝑐𝑧2

El coseno dará siempre entre 0 y 1
El producto escalar varía como máximo entre él 𝑎 . 𝑏 y 0
El coseno nos dice si los vectores son paralelos o perpendiculares
Si coseno de a y b = 0 vectores perpendiculares.
Si coseno de a y b <> 0 vectores perpendiculares.
En este caso, a · b = 0, podemos sacar como conclusión que 𝑎 0 ó 𝑏 = 0, o
bien que a y b son mutuamente perpendiculares.

Módulo de un Vector
Un vector no solo nos da una dirección y un sentido, sino también una magnitud, a
esa magnitud se le denomina módulo.
Gráficamente: es la distancia que existe entre su origen y su extremo, y se
representa por:

Coordenadas cartesianas: En muchas ocasiones es conveniente tomar
las componentes sobre tres direcciones mutuamente perpendiculares
OX, OY y OZ que forman un sistema cartesiano tridimensional.
Si tomamos tres vectores unitarios, i sobre OX, j sobre OY y k sobre OZ,
entonces podemos encontrar puntos ax, ay, az sobre OX, OY, OZ,
respectivamente, tales que:

y aplicando el teorema de Pitágoras nos encontramos con que el módulo de a es:

1.7 APLICACIONES FISICAS Y GEOMETRICAS
DE LOS PRODUCTOS ESCALARES Y
VECTORIALES
Aplicación: ángulo entre dos vectores (producto escalar): El producto escalar de
dos vectores es por definición un escalar.
𝑎 . 𝑏 = 𝑎 . 𝑏 . cos 𝛼
Propiedades:
𝑎 · 𝑏 = 𝑏 · 𝑎
𝑝 · (𝑞 + 𝑟) = 𝑝 · 𝑞 + 𝑝 · 𝑟
Podemos usar ahora el producto escalar para encontrar el ángulo de los
vectores a y b:
𝑎 . 𝑏 = 𝑎 . 𝑏 . cos 𝛼
Con lo que deducimos que:
𝑎𝑥 𝑏𝑥 + 𝑎𝑦 𝑏𝑦 + 𝑎𝑧 𝑏𝑧
𝑎 .𝑏
cos 𝑎, 𝑏 =
=
𝑎. 𝑏
𝑎𝑥2 + 𝑎𝑦2 + 𝑎𝑧2 + 𝑏𝑥2 + 𝑏𝑦2 + 𝑐𝑧2

El coseno dará siempre entre 0 y 1
El producto escalar varía como máximo entre él 𝑎 . 𝑏 y 0
El coseno nos dice si los vectores son paralelos o perpendiculares
Si coseno de a y b = 0 vectores perpendiculares.
Si coseno de a y b <> 0 vectores perpendiculares.
En este caso, a · b = 0, podemos sacar como conclusión que 𝑎 0 ó 𝑏 = 0, o
bien que a y b son mutuamente perpendiculares.

Módulo de un Vector
Un vector no solo nos da una dirección y un sentido, sino también una magnitud, a
esa magnitud se le denomina módulo.
Gráficamente: es la distancia que existe entre su origen y su extremo, y se
representa por:

Coordenadas cartesianas: En muchas ocasiones es conveniente tomar
las componentes sobre tres direcciones mutuamente perpendiculares
OX, OY y OZ que forman un sistema cartesiano tridimensional.
Si tomamos tres vectores unitarios, i sobre OX, j sobre OY y k sobre OZ,
entonces podemos encontrar puntos ax, ay, az sobre OX, OY, OZ,
respectivamente, tales que:

y aplicando el teorema de Pitágoras nos encontramos con que el módulo de a es: